AVL트리란
이진탐색 트리의 단점을 보완하고자 나온 트리이다.
이진탐색 트리의 큰 문제점은 한쪽 방향으로 노드가 쏠릴 수 있다는것이다.
저장하는 순서에 따라 발생되는문제인데
예를 들어 1, 2, 3, 4, 5, 6을 순서대로 저장한다고 하면 오른쪽 으로만 노드가 쏠려버리게되어 성능이 매우 나빠진다.
AVL트리는 이런 이진트리의 단점을 보완이자 극복해준다.
특징
- 이진탐색 트리의 속성을 가진다.
- 왼쪽, 오른쪽 서브 트리의 높이 차이가 최대 1이다.
- 높이 차이가 1보다 커지면 회전을 통해 균형을 맞춰 높이 차이를 줄인다.
- 삽입, 삭제, 검색의 시간복자잡도가 O(logn)이다.
상태
- LL상태

왼쪽 서브트리로 노드가 치우쳐있을때 사용하는 방식으로 오른쪽으로 회전하여 균형을 맞춘다.
순서
y노드의 오른쪽 자식 노드를 z노드로 변경한다.
z노드의 왼쪽 자식노드를 y노드 오른쪽 서브트리(T2)로 변경한다.
y노드가 새로운 루트노드가 된다.
struct node *rightRotate (struct node *z) {
struct node *y = z->left;
struct node *T2 = y->right;
// right 회전 수행
y->right = z;
z->left = T2;
// 노드 높이 갱신
z->height = 1 + max(z->left->height, z->right->height);
y->height = 1 + max(y->left->height, y->right->height);
// 새로운 루트 노드 y를 반환
return y;
}
-RR상태

오른쪽 서브트리로 노드가 치우쳐있을때 사용하는 방식으로 왼쪽으로 회전하여 균형을 맞춘다.
과정
y노드의 왼쪽 자식노드를 z노드로 변경한다.
z노드의 오른쪽 자식노드를 y노드 왼쪽 서브트리(T2)로 변경한다.
y노드가 새로운 루트 노드가 된다.
struct node *leftRotate (struct node *z) {
struct node *y = z->right;
struct node *T2 = y->left;
// left 회전 수행
y->left = z;
z->right = T2;
// 노드 높이 갱신
z->height = 1 + max(z->left->height, z->right->height);
y->height = 1 + max(y->left->height, y->right->height);
// 새로운 루트 노드 y를 반환
return y;
}
-LR 상태

과정
y는 z의 왼쪽 자식 노드이고, x는 y의 오른쪽 자식 노드인 경우
left , right 순으로 총 두 번의 rotation을 수행하여 균형을 맞춘다.
y = z->left;
y = leftRotate(y);
z = rightRotate(z);
-RL상태
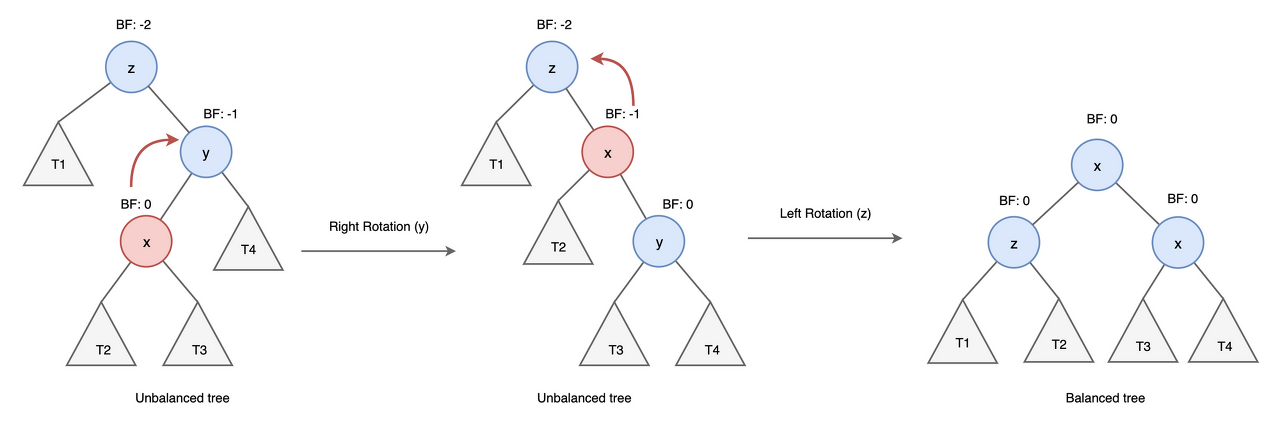
과정
y는 z의 오른쪽 자식 노드이고, x는 y의 왼쪽 자식 노드인 경우
right, left 순으로 총 두번의 rotation을 수행하여 균형을 맞춘다.
y = z->right;
y = rightRotate(y);
z = leftRotate(z);
삽입
AVL트리의 삽입, 삭제 방식은 이진 탐색트리와 동일하지만 삽입, 삭제 후 트리의 균형을 맞추는 함수가 추가된다.
(삭제 부분은 삽입과 동일하므로 생략)
// 삽입 함수.
struct node* insert(struct node* root, int key) {
// 삽입 수행
if (root == NULL)
return newNode(key);
if (key > root->data)
root->right = insert(root->right, key);
else if (key < root->data)
root->left = insert(root->left, key);
else
return root;
// 노드 높이 갱신
root->height = 1 + max(node->left->height, node->right->height);
// 노드 균형 유지
root = rebalance(root);
return root;
}
참고 링크 : https://code-lab1.tistory.com/61
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] 이진탐색 트리(Binary Search Tree) (0) | 2024.01.17 |
|---|---|
| [자료구조] 보간 탐색(Interpolation Search (0) | 2024.01.16 |
| [자료구조] 이진 탐색(Binary Search) (0) | 2024.01.16 |
| [자료구조] 기수정렬(Radix Sort) (0) | 2024.01.15 |
| [자료구조] 퀵 정렬(Quick Sort) (0) | 2024.01.15 |